集合知识点
前言
相关概念
- 元素与集合
1、集合元素的性质:确定性、互异性比如对方程\(x^2\)\(-\)\(2x\)\(+\)\(1\)\(=0\)而言,在初中我们认为有两个相同解,而不认为只有一个解;如果其解集用集合刻画,则必须写成\(\{1\}\),是个单元素集合,而不能写成\(\{1,1\}\);、无序性
2、集合与元素的关系:\(a\in\{a\}\),\(b\notin\{a\}\),
3、集合的表示方法:列举法、描述法、图示法;数集的表示方法还要添加字母法、区间法。
注意区分\(\varnothing\)、\(\{0\}\)、\(\{\varnothing\}\),其中集合\(\{0\}\)、\(\{\varnothing\}\)都是单元素集合,\(\varnothing\)里面没有一个元素。
以下写法都是对的:\(\varnothing\in\{\varnothing\}\),空集是以空集为元素的集合的元素,在特定条件下是成立的;
\(\varnothing\subseteq\{\varnothing\}\),空集是任何集合的子集;\(\varnothing\subsetneqq\{\varnothing\}\),空集是任何非空集合的真子集;
4、常见数集的字母表示及其关系:\(N^*(N_+)\subsetneqq N\subsetneqq Z \subsetneqq Q \subsetneqq R \subsetneqq C\)
- 集合关系
子集:\(x\in A\Rightarrow x\in B\),则\(A\subseteq B\)。
真子集:\(A\subseteq B,\exists x\in B,x\notin A\),则\(A \subsetneqq B\)
相等:\(A\subseteq B,B\subseteq A\Longleftrightarrow A=B\)
空集:\(\forall x\notin \varnothing,\varnothing\subseteq A\)
- 集合运算
交集:\(\{x\mid x\in A且x\in B\}\);
并集:\(\{x\mid x\in A或x\in B\}\);
补集:\(\{x\mid x\in U且x\notin A\}=\complement_UA\);
- 集合性质
并集的性质:\(A\cup\varnothing=A\);\(A\cup A=A\);\(A\cup B=B\cup A\);\(A\subseteq B\Longleftrightarrow A\cup B=B\);
交集的性质:\(A\cap\varnothing=\varnothing\);\(A\cap A=A\);\(A\cap B=B\cap A\);\(B\subseteq A\Longleftrightarrow A\cap B=B\);
补集的性质:\(A\cup(\complement_UA)=U\);\(A\cap(\complement_UA)=\varnothing\);\(\complement_U(\complement_UA)=A\);\(\complement_U(A\cup B)=(\complement_UA)\cap(\complement_UB)\);\(\complement_U(A\cap B)=(\complement_UA)\cup(\complement_UB)\);
- 集合分类
我们根据集合的元素的特点,将其分为数集、点集、式集、图形集、向量集等等,这样我们在区分集合时就变得很容易;比如,
集合\(A=\{ x\mid y=x^2+3x-2\}\),实质是数集,就是函数\(y=x^2+3x-2\)的定义域;
集合\(B=\{y\mid y=x^2+3x-2\}\),实质是数集,就是函数\(y=x^2+3x-2\)的值域;
集合\(C=\{(x,y)\mid y=x^2+3x-2\}\),实质是点集区分点集和数集,主要看代表元素,若是数\(\;x\;\)[往往对应方程的根,不等式的解集,或函数的定义域]或\(\;y\;\)[往往对应值域]则为数集,若是有序数对则为点集;\(\quad\),就是函数\(y=x^2+3x-2\)图像上的所有点构成的点集合;此时如果求\(A\cap C=\varnothing\);
集合\(D=\{x^2,x^2+2y-1,t^3+1\}\),实质是代数式集合,简称式集;
集合\(E=\{\)三角形\(\}\),实质是图形集合;
集合\(F=\{\vec{a},\vec{b},\vec{c},\vec{d}\}\),实质是向量集合;
当然,集合还可以根据其元素的有限与无限分为有限集和无限集。
- 注意区别刻画集合的描述法和列举法
集合\(A=\{x\in N\mid x\leq \sqrt{10}\}\),这是用描述法表达的,当然还可以简化为用列举法表示,比如\(A\)\(=\)\(\{x\)\(\mid\)\(x\)\(=\)\(0\)\(,\)\(1\)\(,\)\(2\)\(,\)\(3\)\(\}\),这时候我们甚至可以写的更简单,比如\(A=\{0,1,2,3\}\)。
常用结论
- 含有\(n\)个元素的集合\(\{a_1,a_2,\cdots,a_n\}\),其所有的子集个数有\(2^n\)个。
解释:从含有\(n\)个元素的集合中分别取\(0\)、\(1\)、\(2\)、\(\cdots\)、\(n\)个元素,则构成的集合的子集的个数分别为\(C_n^0\)、\(C_n^1\)、\(C_n^2\)、\(\cdots\)、\(C_n^n\)个,故所有的子集的个数有\(C_n^0+C_n^1+C_n^2+\cdots+C_n^n=2^n\);
所有的真子集个数有\(2^n-1\)个,即去掉\(C_n^n\)的那一个;所有的非空子集个数有\(2^n-1\)个。即去掉\(C_n^0\)的那一个;所有的非空真子集个数有\(2^n-2\)个。即去掉\(C_n^0=1\)和\(C_n^n=1\)那两个。
- 二项式定理\((a+b)^n=C_n^0a^nb^0+C_n^1a^{n-1}b^1+C_n^2a^{n-2}b^2+\cdots+C_n^ka^{n-k}b^k+\cdots+C_n^na^0b^n\);
当令\(a=b=1\)时,上式即为\(C_n^0+C_n^1+C_n^2+\cdots+C_n^n=(1+1)^n=2^n\);
分析:由题意可知,集合 \(A=\{1,2\}\),集合 \(B=\{1,2,3,4,5\}\),又由于 \(A\subseteq M\subseteq B\),
则集合\(M\)的元素最少有两个,应该是用元素\(1\),\(2\)保底,在此基础上,再从\(3\),\(4\),\(5\)三个元素中选取部分元素添加进去即可,
添加的元素最少应该是\(0\)个,最多是三个,故本题目等价于集合\(\{3,4,5\}\)的所有子集的个数\(C_3^0\)\(+\)\(C_3^1\)\(+\)\(C_3^2\)\(+\)\(C_3^3\),故应该是\(2^3=8\)个;
为便于理解,列举如下:\(\{1,2\}\)、\(\{1,2,3\}\)、\(\{1,2,4\}\)、\(\{1,2,5\}\)、\(\{1,2,3,4\}\)、\(\{1,2,3,5\}\)、\(\{1,2,4,5\}\)、\(\{1,2,3,4,5\}\);
解后反思:注意符号语言 \(A\subseteq M\subseteq B\) 向文字语言的转化。
自定义概念
集合\(A=\{x\mid -2\leq x\leq 7\}\),由于其左右端点是固定不变化的,故我们可以形象的称其为定集;集合\(B\)\(=\)\(\{\)\(x\)\(\mid\)\(m+1\)\(<\)\(x\)\(<\)\(2m-1\)\(\}\),其左右端点是随着\(m\)的取值变化的,故我们可以形象的称其为动集;这样两个集合的关系就可能随着\(m\)的取值发生变化。
仿二次方程:比如\(ax^2+3x-2=0\),由于题目没有告诉\(a\)的取值,那么它就可能是一次方程\(3x-2=0\),也可能是二次方程\(ax^2+3x-2=0(a\neq 0)\),故当我们看到仿二次方程时,我们就应该想到分类讨论,由于思维定势的缘故,最容易漏掉\(a=0\)的情形;
以此类推,\(y=ax^2+3x-2\)就是仿二次函数,包含了一次函数和二次函数两种情形;\(ax^2+3x-2\ge 0\)就是仿二次不等式,包含了一次不等式和二次不等式两种情形;很显然题目中出现这个就是想看看,你的思维是否严密。
分析:由于\(ax^2+2x+1=0\),\(a\in R\),则所给的方程为仿二次方程,故需要针对\(a\)分类讨论,
①当\(a=0\)时,方程变化为\(2x+1=0\),则解集为单元素集合\(\{-\cfrac{1}{2}\}\),满足题意;
②当\(a\neq 0\)时,方程\(ax^2+2x+1=0\)为二次方程,又要求其解集为单元素集合,则必须\(\Delta=0\),即\(2^2\)\(-\)\(4a\)\(=\)\(0\),即\(a=1\),此时方程变为\(x^2\)\(+\)\(2x\)\(+\)\(1\)\(=0\),解集为单元素集合\(\{-1\}\);
加深认识
重新认识集合的作用和地位,主动使用集合工具刻画数学素材
用集合工具来刻画点集
直线比如\(\{(x,y)\mid 2x-y+1=0\}\);曲线比如\(\{(x,y)\mid x^2+y^2=4\}=\{(2cos\theta,2sin\theta)\}\);
比如\(\{(x,y)\mid \cfrac{x^2}{9}+\cfrac{y^2}{4}=1\}=\{(3cos\theta,2sin\theta)\}\);
交点比如\(\{(x,y)\mid \begin{cases} 2x+y-1=0\\ 3x-y+2=0\end{cases} \}\);平面区域比如\(\left\{(x,y)\mid \begin{cases}x^2+y^2\leq 4\\ x\ge 0\\ y\ge0\end{cases}\right\}\);
用集合工具来刻画函数的性质
定义域比如\(\{x\mid y=x^2-3x-2\}=R\);
值域比如\(\{y\mid y=x^2+2\}=[2,+\infty)\);
单调性比如函数\(y=f(x)\)上的任意两个点\((x_1,y_1)\)、\((x_2,y_2)\)满足条件,若\(x_1>x_2\),则必有\(y_1>y_2\),也即意味着函数是单调递增的;也就是当\(x_1>x_2\)时,有\(f(x_1)>f(x_2)\)成立;
奇偶性比如函数\(y=f(x)\)上的任意两个点\((x_1,y_1)\)、\((x_2,y_2)\)满足条件,若\(x_1+x_2=0\),则必有\(y_1=y_2\),也即意味着函数是偶函数;也就是满足\(f(-x)=f(x)\);
对称性比如函数\(y=f(x)\)上的任意两个点\((x_1,y_1)、(x_2,y_2)\)满足条件,若\(x_1+x_2=2\),则必有\(y_1+y_2=2\),也即意味着函数是关于点\((1,1)\)对称的;也就是满足\(f(2-x)+f(x)=2\);
用集合工具来刻画数集
方程的根比如\(\{x\mid x^2-3x+2=0\}=\{1,2\}\);
不等式的解集比如\(\{x\mid x^2-3x+2\leq 0\}=[1,2]\);
用集合工具来表示其他的集合
无理数集合比如\(\complement_RQ\);
集合的并集\(\{x\mid x=2k,k\in Z\}\cup\{x\mid x=2k+1,k\in Z\}=Z\)
角的集合的并集\(\{x\mid x=2k\pi+\cfrac{\pi}{4},k\in Z\}\cup\{x\mid x=(2k+1)\pi+\cfrac{\pi}{4},k\in Z\}=\{x\mid x=k\pi+\cfrac{\pi}{4},k\in Z\}\)
题型方法
1、利用集合之间的关系求参数的取值时,解题后要进行检验,防止不满足集合元素的确定性和互异性;
分析:①当\(a^2-a-1=-1\)时,即\(a^2-a=0\),解得\(a=0\)或\(a=1\);
当\(a=1\)时,\(\{2,a^2-a-1,a^2+1\}=\{2,-1,2\}\),与元素的互异性矛盾,舍去;故\(a=0\)
②当\(a^2+1=-1\)时,\(a^2=-2\),\(a\)无实数解,
由①②可得,\(a=0\),故选\(B\).
分析:由\(a^2-a\neq 2a\),解得\(a\neq 0\)且\(a\neq 3\).
2、要重视符号语言和文字语言之间的相互转化。
3、集合的运算问题的常用策略:充分利用数轴和韦恩图,数形结合。
失误防范
- 解题时注意区分两大关系:一是元素与集合的从属关系;二是集合与集合的包含关系。
- 解答集合题目,认清集合元素的属性(点集,数集,或其他)和化简集合是正确求解的两大先决条件。
- 常用韦恩图示法和数轴图示法解决集合的交、并、补集运算,利用数轴图示法时要注意端点的实心或空心。
- 要注意这五个关系的等价性:
- 题目中出现\(A\subseteq B\)时,常常意味着集合\(A\)有两种情形:\(A=\varnothing\)和\(A\neq \varnothing\)。

\(A\subseteq B\Longleftrightarrow A\cap B=A\);\(A\subseteq B\Longleftrightarrow A\cup B=B\);
- 由集合关系求参数的取值范围时,给定\(A\subseteq B\)和\(A\subsetneqq B\)的求解是有区别的,后者常常需要验证排除使得\(A=B\)的参数值。
本来针对\(A\subsetneqq B\)列不等式组时,应该分类讨论,但我们觉得太麻烦,常常直接依照\(A\subseteq B\)来列不等式组,最后添加一个口算验证即可,这样省事的多。
分析:由\(B\subsetneqq A\),则\(\{x\mid m<x<m+3\}\subsetneqq \{x\mid -4<x<1\}\),
由题目可先直接得到\(\left\{\begin{array}{l}{-4\leqslant m}\\{m+3\leqslant 1}\end{array}\right.\),从而解得\(-4\leqslant m\leqslant -2\),
然后口算验证,当\(m=-4\)时,\(A=(-4,1)\),\(B=(-4,-1)\),满足题意,同理当\(m=-2\)时也满足题意,
故\(m\)的取值范围为\([-4,-2]\)。
- 涉及两个集合的关系时,端点值能否取到是个高频易错点。如已知\(B \subseteq A\),
①当\(A=[-3,1]\),\(B=[1+2m,m+1]\)时,应该得到\(\left\{\begin{array}{l}{-3\leqslant 1+2m}\\{m+1\leqslant 1}\end{array}\right.\),即\(m\in [-2,0]\);
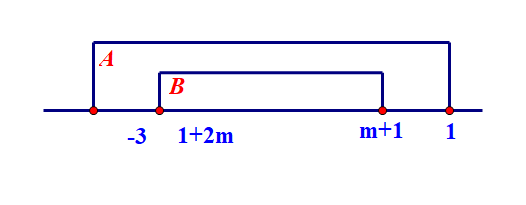
②当\(A=(-3,1)\),\(B=(1+2m,m+1)\)时,应该得到\(\left\{\begin{array}{l}{-3\leqslant 1+2m}\\{m+1\leqslant 1}\end{array}\right.\),即\(m\in [-2,0]\);
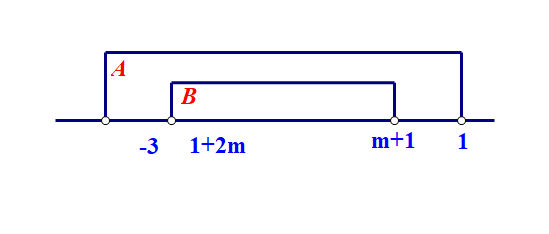
③当\(A=[-3,1]\),\(B=(1+2m,m+1)\)时,应该得到\(\left\{\begin{array}{l}{-3\leqslant 1+2m}\\{m+1\leqslant 1}\end{array}\right.\),即\(m\in [-2,0]\);
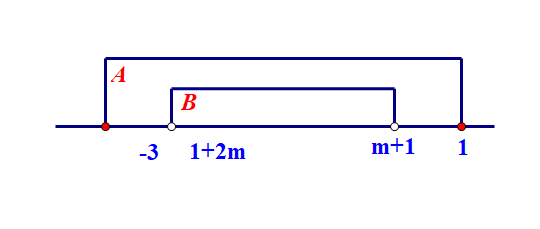
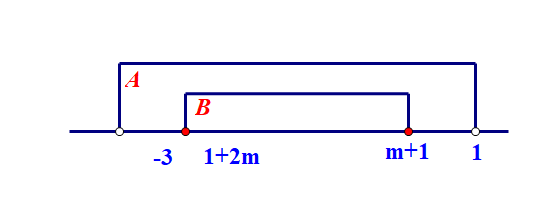
④当\(A=(-3,1)\),\(B=[1+2m,m+1]\)时,应该得到\(\left\{\begin{array}{l}{-3< 1+2m}\\{m+1<1}\end{array}\right.\),即\(m\in (-2,0)\);

 集合知识点
集合知识点
